THEORY OF FLIGHT

So far we have considered the flight of the aircraft following a symmetrical plane. In flight, an aircraft revolve around three axes. In this chapter, we will consider various possibilities of carrying out a turn.

1. FLAT STABLE TURN:

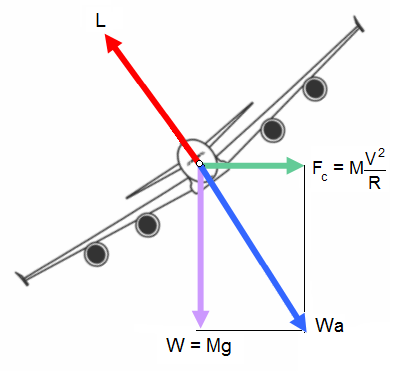
While turning at constant altitude, to avoid side slipping, the pilot uses the rudder. The weight perpendicular to the speed gives rise to the load factor. It is necessary to add the centrifugal force to the forces acting on the aircraft.

The two forces are:

• Weight: W = Mg

• Centrifugal force: (with R being the radius of the turn).

For a perfect turn, the resultant of the two forces remains in the symmetrical plane of the aircraft.

The weight of the airplane remains vertical and is always balanced by the aerodynamic loads. Thus the velocity vector remains in the horizontal plane.

The definition of the load factor (n) is the ratio between the apparent weight of the aircraft and the real weight.

To carry out this turn, the pilot rolls the aircraft. He inclines the aircraft laterally. To avoid side slipping, the pilot operates the rudder. The side slip is controlled by monitoring the roll and bank indicator.

2. SIDESLIP TURN:

To make a sideslip turn, the pilot actuates the rudder. The plane is subjected to an aerodynamic load having a resultant on the Gx axis, on the aerodynamic axes of reference. The realization of the turn is carried out using a larger radius. In fact, this type of turn is used for small bearing changes, about 1 to 2 degrees.

The pilots and passengers are subjected to an unpleasant side acceleration.

3. MAXIMUM PERFORMANCE OF TURN:

Small radius of turn:

The forces in action are applied as shown on the figure, and we obtain:

, with R being the radius of the turn.

From there, we obtain:

^[1]

Remark 1: The radius of the turn is minimum for a maximum load factor at a given speed. The load factor may be applied by the pilot or by the resistance of the aircraft.

Remark 2: ; the load factor is proportional to the square of the speed and inverse-proportional to the radius of the turn.

4. MAXIMUM ANGULAR VELOCITY:

For transport aircraft, the angular velocity is negligible. On the other hand, for fighters, it is interesting to find the necessary parameters to change direction in a minimum period of time.

Consider φ as the angle of reference.

To carry out the change in direction it is necessary to find the maximum value:

n and V are related to lift and thrust.

The angular velocity is maximum for the same angle of attack as for the minimum turning radius.

5. TURN AT CONSTANT SPEED:

By cancelling out common terms from the thrust and lift equations, we obtain:

At each position of the throttle an infinite possible number of turns is possible from n = 1 to a maximum load factor.